MATEMÁTICAS

¿Que son las matemáticas? 

La matemática es la ciencia deductiva que se dedica al estudio de las propiedades de los entes abstractos y de sus relaciones. Esto quiere decir que las matemáticas trabajan con números, símbolos, figuras geométricas, etc.

PROPIEDADES DE LOS POLÍGONOS Y POLIEDROS

¿Que son los polígonos?

Un polígono es la figura geométrica de un plano que está establecida por líneas rectas. Se trata de un fragmento plano que está formado por segmentos consecutivos sin alineación, que reciben el nombre de lados.

CLASIFICACIONES DE LOS POLÍGONOS 

*Polígono simple: Se llama polígono simple al polígono cuyos lados no contiguos no se intersectan, es decir, que dicho polígono es la frontera de la respectiva región poligonal.​ Un polígono simple divide al plano que lo contiene en dos conjuntos de puntos: interior de la región poligonal y exterior de la región poligonal. El interior se caracteriza porque no puede contener una recta; el exterior sí puede contener una recta.

*Polígono complejo:Un polígono complejo, es aquel que no se interseca consigo mismo, es decir sus bordes se cruzan con él mismo por ello tiene más de un borde.

Otros tipos de polígonos son el cóncavo (cuando lo atraviesa una recta puede cortarlo en más de un par de puntos), convexo(al ser atravesado por una línea recta, lo interrumpe en no más de dos puntos), regular (sus lados y ángulos son iguales), irregular (sus lados y ángulos son desiguales), equiángulo(todos sus ángulos resultan iguales) y equilátero (todos sus lados cumplen con la propiedad de la igualdad).

POLÍGONOS REGULARES

Un "polígono regular" tiene todos los lados iguales y todos los ángulos iguales. 

A continuación se muestra un ejemplo del angulo externo, angulo interior y angulo central de un hexágono

ANGULO INTERNO

El ángulo interior de un polígono regular de "n" lados se calcula con la fórmula: (n-2) × 180° / n Por ejemplo el ángulo interior de un octágono (8 lados) es: (8-2) × 180° / 8 = 6×180°/8 = 135° Y el de un cuadrado es (4-2) × 180° / 4 = 2×180°/4 = 90° ANGULO EXTERNO Los ángulos exterior e interior se miden sobre la misma línea, así que suman 180°. Por lo tanto el ángulo exterior es simplemente 180° - ángulo interior El ángulo interior de este octágono es 135°, así que el ángulo exterior es 180°-135° = 45° El ángulo interior de un hexágono es 120°, así que el ángulo exterior es 180°-120° = 60° DIAGONALES Todos los polígonos (menos los triángulos) tienen diagonales (líneas que van de un vértice a otro, pero que no son lados). El número de diagonales es n(n - 3) / 2. A CONTINUACIÓN SE PRESENTA UNA TABLA CON LAS FORMULAS PARA SACAR EL PERÍMETRO Y ÁREA DE LOS POLÍGONOS

LOS POLIGONOS

Polígonos

Un polígono es una figura plana con lados rectos.

¿Es un polígono?

Los polígonos son formas bidimensionales. Están hechos con líneas rectas, y su forma es "cerrada" (todas las líneas están conectadas).

Polígono (lados rectos)	No es un polígono (tiene una curva)	No es un polígono (abierto, no cerrado)

Tipos de polígonos

Simple o complejo

Un polígono simple sólo tiene un borde que no se cruza con él mismo. ¡Uno complejo se interseca consigo mismo!

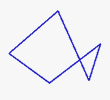Polígono simple (este es un pentágono)	Polígono complejo (también es un pentágono)

Cóncavo o convexo

Un polígono convexo no tiene ángulos que apunten hacia dentro. En concreto, los ángulos internos no son mayores que 180°.

Si hay algún ángulo interno mayor que 180° entonces es cóncavo. (Para acordarte: cóncavo es como tener una "cueva")

Convexo	Cóncavo

Regular o irregular

Si todos los ángulos son iguales y los lados también, es regular, si no es irregular

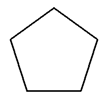Regular	Irregular

Más ejemplos

Polígono complejo (un "polígono estrellado", en este caso un pentagrama)	Octágono cóncavo	Hexágono irregular

Nombres de polígonos

		Si es regular...
Nombre	Lados	Forma	Ángulo interior
Triángulo (o trígono)	3		60°
Cuadrilátero (o tetrágono)	4		90°
Pentágono	5		108°
Hexágono	6		120°
Heptágono (o Septágono)	7		128.571°
Octágono	8		135°
Nonágono (or eneágono)	9		140°
Decágono	10		144°
Endecágono (or undecágono)	11		147.273°
Dodecágono	12		150°
Tridecágono	13		152.308°
Tetradecágono	14		154.286°
Pentadecágono	15		156°
Hexadecágono	16		157.5°
Heptadecágono	17		158.824°
Octadecágono	18		160°
Eneadecágono	19		161.053°
Icoságono	20		162°
Triacontágono	30		168°
Tetracontágono	40		171°
Pentacontágono	50		172.8°
Hexacontágono	60		174°
Heptacontágono	70		174.857°
Octacontágono	80		175.5°
Eneacontágono	90		176°
Hectágono	100		176.4°
Chiliágono	1,000		179.64°
Miriágono	10,000		179.964°
Megágono	1,000,000		~180°
Googológono	10100		~180°
n-ágono	n		(n-2) × 180° / n

Para polígonos con 13 lados o más, se puede escribir (y es más fácil) "13-ágono", "14-ágono" ... "100-ágono", etc. http://www.disfrutalasmatematicas.com/geometria/poligonos.html

Polígonos y poliedros

POLÍGONOS Y POLIEDROS

Veamos las diferencias entre polígonos y poliedros, y los elementos que tienen en común.

Un polígono es la porción de plano limitada por segmentos, por tanto es bidimensional, es decir es plano. Sus elementos son: Lados, vértices, ángulos y diagonales.

Un poliedro es una figura tridimensional (tiene volumen) cuyas caras son polígonos. Sus principales elementos son: Caras, vértices y aristas.
Los prismas y pirámides también son poliedros

os del mundo de los polígonos (figuras planas o bidi-

mensionales) al mundo de los poliedros (cuerpos en el espacio

tridimensional). En el proceso de fabricación de piezas y en

la construcción de edificios tiene especial importancia la

interpretación del plano de la pieza o del edificio, para luego

construir el modelo, réplica de la pieza que se producirá

posteriormente.

Así también construimos cuerpos a partir de sus respectivas

redes o planos, lo que nos permite proyectar edificios y estruc-

turas de uso en la construcción y el diseño.

Las figuras representadas son cuerpos geométricos en el espa-

cio, limitados por un número finito de superficies planas.

Estos cuerpos reciben el nombre de poliedros. Las superficies

planas en cuestión son polígonos y se denominan caras del

poliedro.

El mundo de los poliedros

Observa cualquiera de los poliedros que están dibujados y

algunos de sus elementos característicos:

a) ¿Cómo definirías cada uno de sus elementos?

b) ¿Cuántas caras, vértices y aristas tiene?

c) ¿Cuántas caras, como mínimo, habrá que juntar en un

vértice?

d) ¿Cuánto pueden sumar, como máximo, los ángulos de las

caras que concurren en un mismo vértice?

Se denomina orden del vértice al número de caras que con-

curren a un mismo vértice. Este poliedro tiene orden del vér-

tice 3.

Cara

Vértice

Este es un poliedro que tiene 14

vértices, 21 aristas y nueve caras.

Este cuerpo geométrico no es un

poliedro.

¿Por qué el cuerpo de la derecha no es un Los poliedros regulares convexos son conocidos con el nombre de

sólidos platónicos en honor al filosofo griego Platón (428-347 a.C.)

que los cita en el Timeo, pero lo cierto es que no se sabe en que época

llegaron a conocerse. Algunos investigadores asignan el cubo, el

tetraedro y el dodecaedro a Pitágoras (siglo IV a.C.) y el octaedro e

icosaedro a Teeteto (415-369 a.C.). Para Platón los elementos últimos

de la materia son los poliedros regulares, asignando el fuego al tetraedro

(el fuego tiene la forma del tetraedro, pues es el elemento mas pequeño,

ligero, móvil y agudo), la tierra al cubo (el poliedro mas sólido de los

cinco), el aire al octaedro (para los griegos el aire, de tamaño, peso y

fluidez, en cierto modo intermedios, se compone de octaedros) y el

agua al icosaedro (el agua, el más móvil y fluido de los elementos,

debe tener como forma propia o "semilla , el icosaedro, el sólido más

cercano a la esfera y, por tanto, el que con mayor facilidad puede rodar),

mientras que al dodecaedro le asignó el Universo. Como los griegos

ya tenían asignados los cuatro elementos dejaban sin pareja al

dodecaedro, por lo que lo relacionaron con el Universo como conjunción

de los otros cuatro. La forma del dodecaedro es la que los dioses

emplean para disponer las constelaciones en los cielos. Dios lo utilizó

para todo cuando dibujó el orden final.

En cada uno de los poliedros abajo representados cuenta el número de

vértices V, el número de aristas A y el número de caras C.

Calcula V-A+C. ¿Qué número se obtiene? La relación resultante fue

demostrada por Euler.

El mundo de los poliedros regulares

Hexaedro regular

o cubo

Tetraedro regular Dodecaedro

regular

Poliedro regular Icosaedro regular Octaedro regular

Modelo

Caras

Vértices

Aristas

Aristas por

vértice

6 cuadrados

8

12

3

4 triángulos

equiláteros

4

6

3

20

30

3

12

30

5

6

12

https://poli-poligo/mate/123.com?

LOS POLIEDROS 

Poliedros

Los poliedros son cuerpos geométricos que tienen todas sus caras formadas por polígonos. Muchos objetos de nuestro alrededor tienen forma de poliedro:

Los elementos de un poliedro son caras, vértices y aristas.

• Las caras son los polígonos que la limitan.
• Las aristas son los lados de las caras, y limitan dos caras contiguas.
• Los vértices son los de las caras. En cada vértice de un poliedro concurren tres o más caras.
• Diagonales: Segmentos que unen dos vértices no pertenecientes a la misma cara.

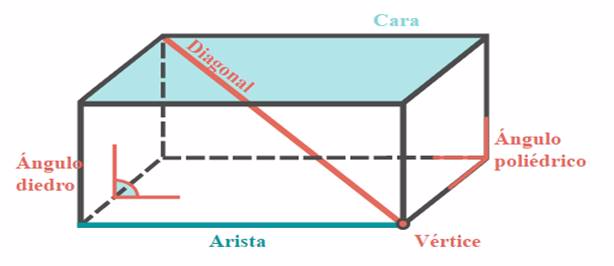
 Los ángulos que están dentro de los políedros pueden ser:

• Ángulo diedro: Es la proporción de espacio limitada por dos semiplanos que se llaman caras.

• Ángulo poliedro: Es la proporción de espacio limitada por tres o más planos que concurren en un punto llamado vértice. Un ángulo poliedro debe medir menos de 

Para finalizar, en todos los poliedros se cumple la llamada Relación de Euler: Siendo   el número de caras del poliedro,   el número de vértices del poliedro y   el número de aristas.

Clasificación y familias de poliedros

Los poliedros pueden ser clasificados en muchos grupos según la familia dónde provienen o de las características que los diferencian. Según sus características, se distinguen:

• En un poliedro convexo una recta sólo pueda cortar a su superficie en dos puntos.

• En un poliedro cóncavo una recta puede cortar su superficie en más de dos puntos, por lo que posee algún ángulo diedro entrante.



• En un poliedro de caras regulares todas las caras del poliedro son polígonos regulares.

• En un poliedro de caras uniformes todas las caras son iguales.



• Se dice poliedro de aristas uniformes cuando en todas sus aristas se reúnen el mismo par de caras.



• Se dice poliedro de vértices uniforme cuando en todos los vértices del poliedro convergen el mismo número de caras y en el mismo orden.

 Estos grupos no son exclusivos, es decir, un poliedro puede estar incluido en más de uno de ellos.

Además de las clasificaciones anteriores, también podemos clasificar los poliedros mediante sus familias: Poliedros regulares: Son los llamados sólidos platónicos. Poliedro cuyas caras son polígonos regulares iguales y todas sus aristas son de igual longitud; en consecuencia, todos sus vértices están contenidos en una esfera. Los poliedros regulares son cinco y se denominan:

• tetraedro regular: poliedro regular definido por 4 triángulos equiláteros iguales,
• hexaedro regular (cubo): poliedro regular definido por 6 cuadrados iguales,
• octaedro regular: poliedro regular definido por 8 triángulos equiláteros iguales,
• dodecaedro regular: poliedro regular definido por 12 pentágonos regulares iguales,
• icosaedro regular: poliedro regular definido por 20 triángulos equiláteros iguales.



https://www.geogebra.org/m/acrcYQNj